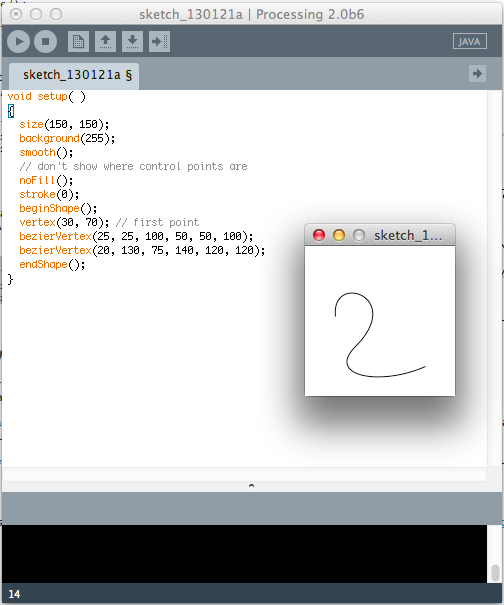
A String osztály
Már használtunk stringet pl. képfájl betöltésére vagy szöveg kiírására, ezek kódjai:
println("printing some text to the message window!");
PImage img = loadImage("filename.jpg");
A string karaktert vagy karakterláncot jelent. A karakterek értéket is tárolnak, tehát a string is adat.
Ha nem lenne string osztályunk akkor ilyen kódot kellene írnunk:
char[] sometext={'H','e','l','l','o',' ','W','o','r','l','d'};
De mivel Processingben van, ezét a következő formát használhatjuk:
String sometext = "How do I make String? Type some characters
between quotation marks!"; //a kódot egy sorba írd!
Különböző metódusokkal működik:
charAt()
Szimpla karater ad vissza, az index szám jelöli hogy a stringnek hanyadik elemét akarjuk kiolvasni. Arra vigyázz hogy az első elemet 0-val, a másodikat 1-gyel stb. lehet elérni!
String message = "some text here.";
char c = message.charAt(3);
println(c); // az eredmény: 'e'
length()
Nem összekeverendő a tömbb hossz paraméterével. A kerek zárójel is arra utal hogy ez nem egy paraméter hanem egy függvény.
String message = "This String is 34 characters long.";
println(message.length());
toUpperCase(), toLowerCase()
Átváltoztathatjuk a stiongünket nagybetűkre és kisbetkre ezekkel.
String uppercase = message.toUpperCase();
println(uppercase);
Mivel a string egy állandó, tehát értéke nem változik, ezért ha változtatni akarjuk akkor mindig létre kell hoznunk egy új stringet. Ebben a példában a a toUpperCase a sting negybetűs másolatát küldi vissza.
equals()
== operátorral tehetjük a stringet valamivelegyenlővé, a szimpla = deklarálásra szolgál!
String one = "hello";
String two = "hello";
println(one == two);
A harmadik sorban az objektumok memória címét hasonlítjuk össze (technikailag), mivel ugyanazta stringet tartalmazzaa kétérték megegyezik, egyébként a végeredmény hamis (false) lenne.
Az equal() függvény biztosítja hogy leellenőrizhessük hogy a két string ugyanazt a karakterláncot tartalmazza-e, figyelmen kívül hagyva hogy hol tároljuk az adatot.
String one = "hello";
String two = "hello";
println(one.equals(two));
Habár mindkét kód ugyanazt csinálja, biztonságosabb az equalt() használni, mivel attól függően hogy a kódban hol hozzuk létre string objektumot, az == nem mindigműködik.
Stingeket egymáshoz is fűzhetünk a + operátorral, számok esetében ez természetesen összeadást jelent.
String helloworld = "Hello" + "World";
Változókat is hozzá fűzhetünk stringekhez:
int x = 10;
String message = "The value of x is: " + x;
Szöveg megjelenítése
Ennek legegyszerűbb modja hakiprinteljük őket az üzenet ablakban. Ezt csináljuk amikor nyomon akarjuk követni az adatunkat, pl. ha a horizontális egérmozgást akarjuk tudni akkor ezt írjuk le:
println(mouseX);
De akár leíró szöveget is kiírhatunk a kódban általunk gondolt helyen:
println("Kiírjuk az egér pozícióját!");
Ebben az esetben a szövegünk még nem a megjelenítő ablakban van, hogyan tudnánk ezt is elérni? A következő pár lépéssel:
1. Deklaráljunk egy PFont típusú objektumot.
PFont f;
2. Hozzuk létre a betűket a nevére hivatkozva a createFont() függvénnyel. Ez ugyanúgy egyszer fut le minta setup(). Éppúgy mint a képeknél, memóriába töltjük az adatot, tehát nem célszerű draw() függvénbe tenni.
Az elérhető rendszer-betűtipusokat (mindenkinek van, nem kell telepíteniük) egy kóddal ki tudod printelni, ezután innen tudsz választani:
size(200, 200);
String[] fontList = PFont.list();
println(fontList);
Ezután a következő szintaxissal tudod alkalmazni a betű-nevedhez a paramétereket: típus, mérte, anti-alising legyen (true) vagy ne (false):
f = createFont("Arial",16,true);
// Arial, 16 pont, anti-aliasing be
3. Specifikáld a betűt a textFont() segítségével, két paramétere van, a betű-változód neve és a mérete (utóbbi opcionális és változtatható). Ez a sima text()-hez képest egy bitmap képet eredményez, így dinamikusan növelhető aszöveg mérete. P2D render használatával feljavíthatod a kép minőségét és teljesítményt is. A P3D render pixeleket eredményezhet.
textFont(f,36);
4. Szín megadása fill()-lel:
fill(255);
5. A szöveget a text() függvény meghívásával tudjuk megjeleníteni. Három paraméterrel rendelkezik, éppúgy mint a formák: a megjelenítendő szöveg, x és y koordinátaák.
text("Hello Strings!",10,100);
A teljes kód:
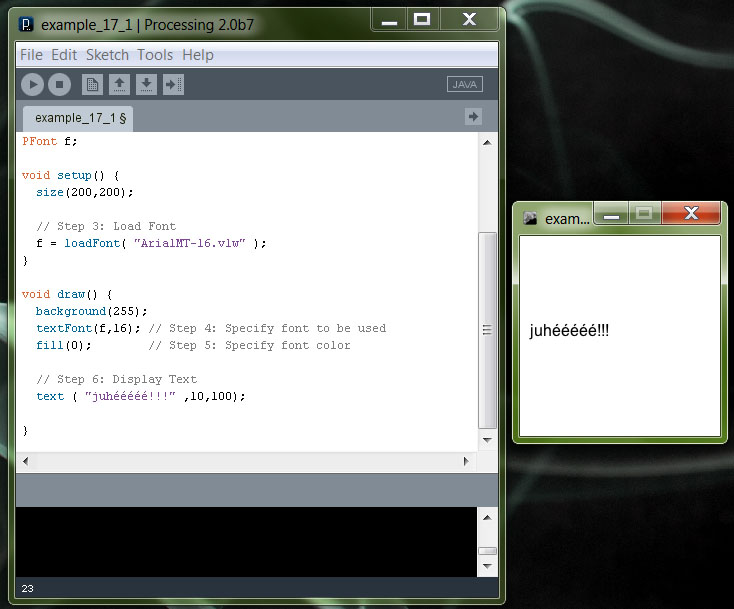
PFont f;
void setup() {
size(200,200);
f = createFont("Arial",16,true);
}
void draw() {
background(255);
textFont(f,16);
fill(0);
text("Hello Strings!",10,100);
}
Menüből is létrehozhatunk betűt: "Tools" --> "Create Font." Ez létrehoz egy VLW betű fájlt a data mappádban, amit PFont objektumba be tudsz tölteni loadFont() függvénnyel.
f = loadFont("ArialMT-16.vlw");
Szöveg animálása
Nézzünk meg néhány hasznos függvényt a fentiek mellé!
textAlign()
A sortördelést határozhatjuk meg vele: balra zárt (LEFT), középre zárt (CENTER) és jobbra zárt (RIGHT).
PFont f;
void setup() {
size(400,200);
f = createFont("Arial",16,true);
}
void draw() {
background(255);
stroke(175);
line(width/2,0,width/2,height);
textFont(f);
fill(0);
textAlign(CENTER);
text("This text is centered.",width/2,60);
textAlign(LEFT);
text("This text is left aligned.",width/2,100);
textAlign(RIGHT);
text("This text is right aligned.",width/2,140);
textWidth()
Kiszámolja és visszaküldi egy karakter vagy szöveg string szélességét.
Csináljuk egy balról jobbra mozgó feliratot! Ha tudjuk a kezdőpont x koordinátáját és a szöveg szélességét, valamint az ablakunk méretét, akkor ki tudjuk számolni az animáció végének x koordinátáját, ahol méglátszik a teljes szöveg.
Először setup()-ban inicializáljuk a szöveget, betűtipust és méretet, x és y koordinátát:
// Főcim animálása
String headline = "Akármi lehet a főcím";
PFont f; // globális változó: f
float x; // szöveg vzsintes pozíciója
void setup() {
f = createFont("Arial",16,true); // betű betöltése
x = width; // inicializáljuk a szöveg jobb szélét
}
A draw()-ban megjelenítjüka szöveget az adott helyen:
textFont(f,16);
textAlign(LEFT);
text(headline,x,180);
Változtatjuk az x pozició értékét hogy létrejöjjön az animáció, mivel balra kell csússzon az értéket csökkentjük:
x = x - 3;
Most egy kicsit bonyolultabb rész jön. Mivel a szövegünk balra van zárva, ezért nem elég ha x kisebb mint 0 egyenlettel akarjuk eltűntetni az ablakból (mint formáknál) mivel ilyenkormég egy része belóg a képe. Ehelyett az egyenletünk úgy néz ki hogy x kisebb mint a nullából kivont szöveg-szélesség (alább a kód):
float w = textWidth(headline);
if (x < -w) {
x = width;
}
A teljes kód:
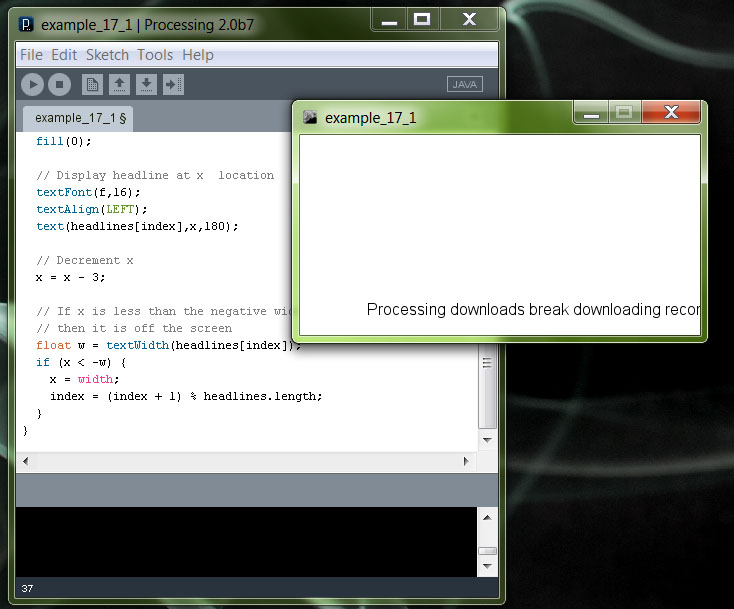
// string tömbbe tesszük a szöveget:
String[] headlines = {
"Processing a köbön",
"Akármi lehet a főcím",
};
PFont f; // f globális betű változó
float x; // szöveg vizszintes helyzte
int index = 0;
void setup() {
size(400,200);
f = createFont("Arial",16,true);
// jobboldali szöveg eltűntetés inicializálása
x = width;
}
void draw() {
background(255);
fill(0);
// szöveg megjelenítése x poziciónál
textFont(f,16);
textAlign(LEFT);
text(headlines[index],x,180);
// animáció sebessége:
x = x - 3;
// ha x kisebb minta negatv szélesség
// tűnjön el a szöveg:
float w = textWidth(headlines[index]);
if (x < -w) {
x = width;
index = (index + 1) % headlines.length;
}
}
Ezeken kívül még a textLeading(), textMode(), textSize() függvények tartoznak a témához.
Szöveg forgatása
Transzformációt és forgatást is érvényesíthetünk szövegre. Tanslate() használatakor a koordinátarendszerünket helyezzük alrébb, így a fomra x,y értéke ugyanaz maradhat:
A pushMatrix() és popMatrix() függvényekkel jelezzük hogy a transzformációt melyik parancssorokra akarjuk értelmezni (amennyiben nem az egész kódra akarjuk). A példában a kirajzolt szürke négyszöget eltoljuk translate()-tel ráccsal együtt 60,80 koordinátához és kékre színezzük, amint látod ennek helye megegyezik a másodiknak kirajzolt piros négyzettel, amit az eredeti koordinátarendszerben rajzoltunk ki, csak a kezdőpontját helyeztük át, mivel minkét négyszög elfás,a színeik összekeverednek, így egy lila jön létre:
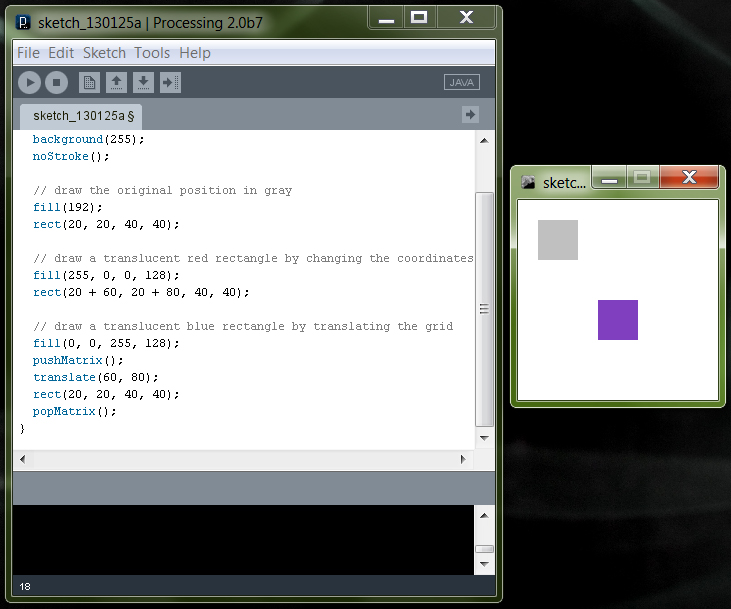
void setup()
{
size(200, 200);
background(255);
noStroke();
// eredeti szürke négyzet kirajzolása:
fill(192);
rect(20, 20, 40, 40);
// az átlátszó piros nyégyzet megváltoztatott koordinátával:
fill(255, 0, 0, 128);
rect(20 + 60, 20 + 80, 40, 40);
// az átlátszó kék négyzet a rács alrébb tolásával:
fill(0, 0, 255, 128);
pushMatrix();
translate(60, 80);
rect(20, 20, 40, 40);
popMatrix();
}
A forgatás ugyanígy működik, paraméternek megadjuk hogy milyen mértékegységben és mennyivel akarjuk forgatni:
pushMatrix();
rotate(radians(45));
fill(0);
rect(40, 40, 40, 40);
popMatrix();
Nagyítás vagy kicsinyítés:
pushMatrix();
scale(2.0);
rect(20, 20, 40, 40);
popMatrix();
Az előzőek alapján forgassuk körbe a középpont körül a középre igazított szövegünket:
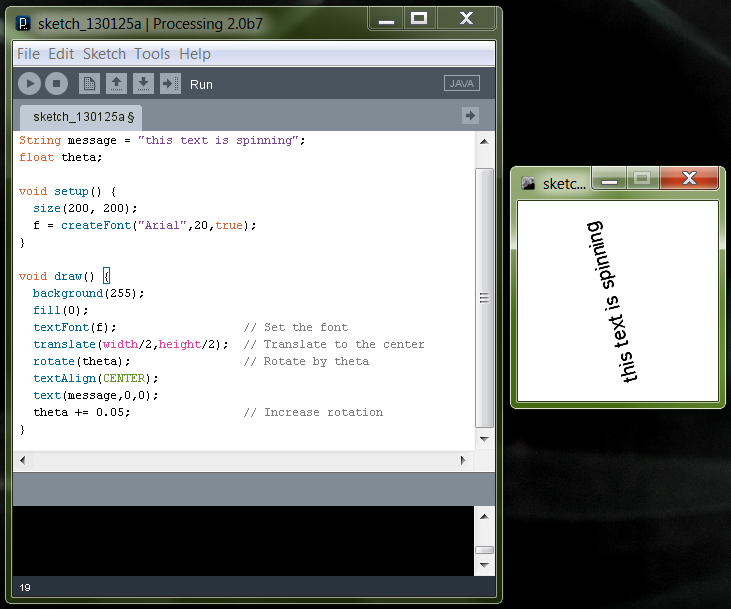
PFont f;
String message = "ez a szöveg pörög";
float theta;
void setup() {
size(200, 200);
f = createFont("Arial",20,true);
}
void draw() {
background(255);
fill(0);
textFont(f); // szöveg beállítása
translate(width/2,height/2); // középre transzformálása
rotate(theta); // elforgatása theta-változó értékével
textAlign(CENTER);
text(message,0,0);
theta += 0.05; // forgatás növelése
}
Szöveg kirajzolása karakterenként
Ebben az esetben a karaktereket egyenként mozgathatod, színezheted, stb. Ehhez létre kell hoznod egy tömbböt amibe beolvasod a karaktereket egyenként charAt() függvénnyel, és innen fogod őket kirajzolni úgy hogy a pozíciójuk x tengelyen mindig 10-zel több. A fent említett módokon hozd létre a PFont objektumodat, töltsdbele a szöveget, határozd meg aszöveg tulajdonságait és draw()-ba írd a karakter számláló for ciklust!
PFont f;
String message = "Each character is not written individually.";
void setup() {
size(400, 200);
f = createFont("Arial",20,true);
}
void draw() {
background(255);
fill(0);
textFont(f);
// egy tömbként jelenik meg a szöveg
text(message,10,height/2);
}
Ebben az esetben egyben jelent meg a szöveged, mivel nincs kiolvasva karakterenként. Írjuk át:
PFont f;
String message = "Each character is written individually.";
void setup() {
size(400, 200);
f = createFont("Arial",20,true);
}
void draw() {
background(255);
fill(0);
textFont(f);
int x = 10;
for (int i = 0; i < message.length(); i++) {
// i++ ugyanaz mint i=i+1
// charAt() egyesével beolvassa a karaktereket:
text(message.charAt(i),x,height/2);
// 10 pixelközönként kiírja a karaktereket:
x += 10;
}
}
Ebben az esetbenmár karakterenkéntírtuk ki a szöveget,de nagyon szétesik, igazítsuk meg textWidth() fügvénnyel, ami kiolvassa az adott karakter (i változóval meghatározott) szélességét (pixelben) és hozzáadja az x-hez (ami10 pixel):
PFont f;
String message = "Each character is written individually.";
void setup() {
size(400, 150);
f = createFont("Arial",20,true);
}
void draw() {
background(255);
fill(0);
textFont(f);
int x = 10; //első karakter itt lesz
//kiolvassuk a karaktereket sorban egy for ciklussal:
//
for (int i = 0; i < message.length(); i++) {
textSize(random(12,36)); // 12-36 közötti random érték
text(message.charAt(i),x,height/2);
// textWidth() a betűköz helyes beállítására:
x += textWidth(message.charAt(i));
}
noLoop();
}
Most már tudjuk effektezni is a karaktereket egyenként! Akövetkező példában, ha nyomva tartod a bal egér gombot, akkor összerázódnak a betűk, azaz pozíciót változtatnak:
PFont f;
String message = "click mouse to shake it up";
// Letter objektum tömb, letters névvel:
//Az osztályt később meghatározzuk majd!
Letter[] letters;
void setup() {
size(260, 200);
// betű betöltése
f = createFont("Arial",20,true);
textFont(f);
// adott string hosszúságú tömbb létrehozása:
letters = new Letter[message.length()];
// Letters inicializálása x pozícióra
int x = 16;
for (int i = 0; i < message.length(); i++) {
letters[i] = new Letter(x,100,message.charAt(i));
x += textWidth(message.charAt(i));
}
}
void draw() {
background(255);
for (int i = 0; i < letters.length; i++) {
// betűk megjelenítése
letters[i].display();
// ha egérgomb nyomva, a betűk rázkódnak
// ha nincs,akkor eredetipozícióba kerülnek
if (mousePressed) {
letters[i].shake();
} else {
letters[i].home();
}
}
}
// Az osztály ami minden egyes betűre jellemző
class Letter {
char letter;
// jegyezze meg az eredeti pozícióját:
float homex,homey;
// és a pillanatnyit is:
float x,y;
Letter (float x_, float y_, char letter_) {
homex = x = x_;
homey = y = y_;
letter = letter_;
}
// betűk megjelentése
void display() {
fill(0);
textAlign(LEFT);
text(letter,x,y);
}
// mozgasd a betűket random
void shake() {
x += random(-2,2);
y += random(-2,2);
}
// kerüljenek vissza a betűk eredeti pozícióba
void home() {
x = homex;
y = homey;
}
}
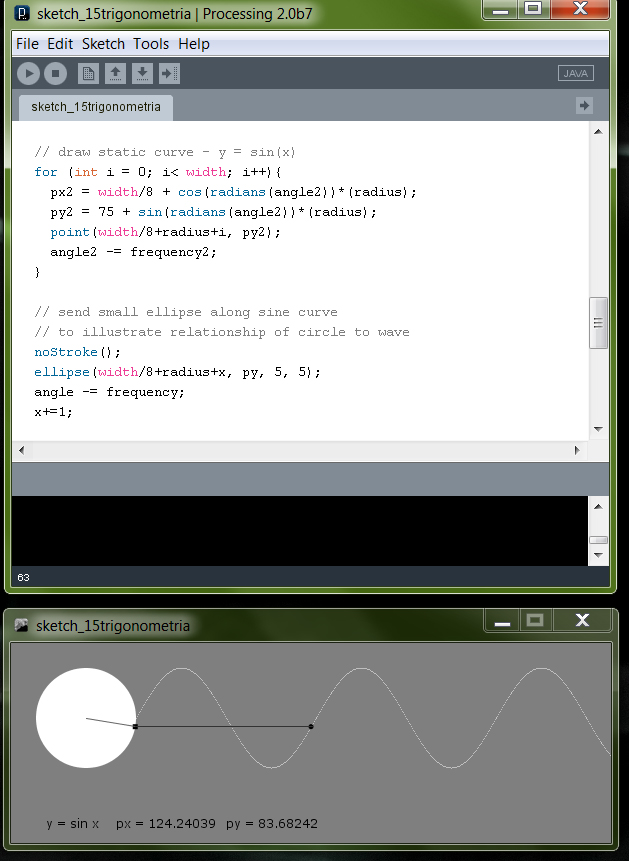
A karakterről karakterre módszer lehetővé teszi hogy görbére illesszük a szöveget. Első lépésként fűzzünk fel négyzeteket egy körvonalra, ehhez trigonometriát kell alkalmaznunk.
Példa:
PFont f;
// A kör sugara:
float r = 100;
// a dobozok szélessége és magassága:
float w = 40;
float h = 40;
void setup() {
size(320, 320);
smooth();
}
void draw() {
background(255);
// Rajzoljunk egy kört az ablak közepére
translate(width / 2, height / 2); //eltoltuk a rácsot
noFill();
stroke(0);
// Az ablakunk közzépontj a köré is,
// innen rajzolunk r sugarú kört:
ellipse(0, 0, r*2, r*2);
// 10 dobozunk legyen:
int totalBoxes = 10;
// Visszakövetjük a pozíciójukat a görbe mentén:
float arclength = 0;
// for ciklus az összes dobozhoz:
for (int i = 0; i < totalBoxes; i++) {
// a dobozok felének szélességével toljuk el őket:
arclength += w/2;
// A fok radiánban megadva,
// a pozíció osztva a sugárral:
float theta = arclength / r;
pushMatrix();
// derékszögű koordináta átalakítása:
translate(r*cos(theta), r*sin(theta));
// doboz elforgatása:
rotate(theta);
// doboz megjelenítése:
fill(0,100);
rectMode(CENTER);
rect(0,0,w,h);
popMatrix();
// ismét elmozdítjuk a dobozt:
arclength += w/2;
}
}
Ezek után a dobozokon belülre helyezzünk egy-egy betűt. Mivel a betűk szélessége változó ismét a textWidth()-et hívjuk segítségül.
// A megjelenítendő szöveg:
String message = "text along a curve";
PFont f;
// a kör sugara:
float r = 100;
void setup() {
size(320, 320);
f = createFont("Georgia",40,true);
textFont(f);
// Középre zárjuk a szöveget:
textAlign(CENTER);
smooth();
}
void draw() {
background(255);
// középre toljuk a koordináta rendszert:
// kört rajzolunk:
translate(width / 2, height / 2);
noFill();
stroke(0);
ellipse(0, 0, r*2, r*2);
// Visszakövetjük a pozíciót a görbe mentén:
float arclength = 0;
// For ciklus az összes dobozhoz:
for (int i = 0; i < message.length(); i++)
{
// leellenőrizzük minden karakter szélességét:
char currentChar = message.charAt(i);
float w = textWidth(currentChar);
// alrébb tesszük a dobozok szélességével:
arclength += w/2;
// radiánsban megadott szög:
// dobozok szélessége osztva a kör sugarával:
// a kör bal szélén kezdjük, PI-től indul:
float theta = PI + arclength / r;
pushMatrix();
// derékszögű koordináta átalakítása:
translate(r*cos(theta), r*sin(theta));
// doboz elforgtása:
rotate(theta+PI/2); // 90 fokkal elforgatjuk
// karakter megjelenítése
fill(0);
text(currentChar,0,0);
popMatrix();
// eltolása a megfelelő pozícióhoz:
arclength += w/2;
}
}
A fokok PI-vel meghatározott értékei:
forrás: http://processing.org/learning/text/,
http://processing.org/learning/transform2d/
http://processing.org/reference/pushMatrix_.html
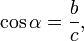
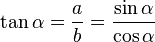
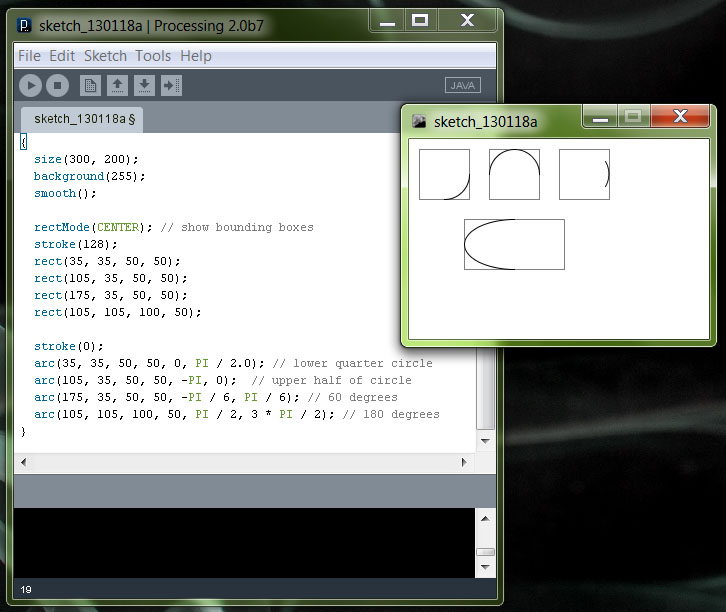
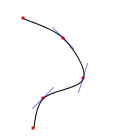
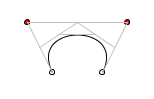
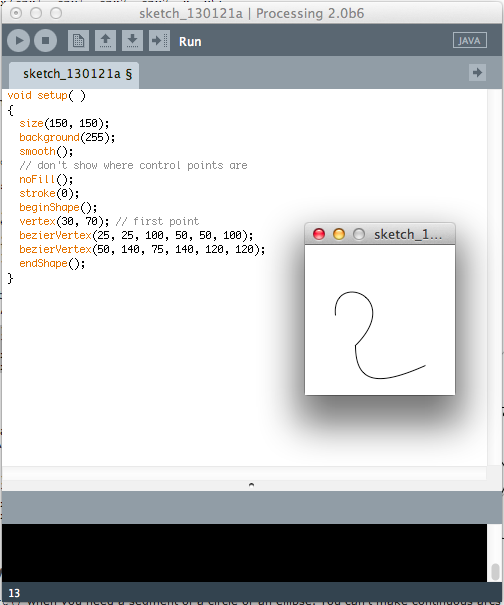
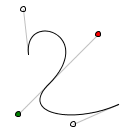
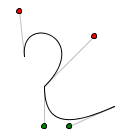Ezért a második ívrész első kontroll pontját alrébb kell tennünk:
