Processing leckék

A grafikus programozás legfőbb része a trigonometria, ami a síkgeometriában a a derékszügű háromszög oldalai és szögei közötti összefüggéseket vizsgálja. 

A könnyebb megjegyezhetőség kedvéért mozaikszavakat is alkalmazhatunk:

hypotenuse-átfogó, opposite-ellentétes (a szöggel szemközti), adjacent-szomszédes

• soh - szinusz
• cah - koszinusz
• toa - tangens

• A szinusz függvény (sin) az α szöggel szemben lévő a befogó és a c átfogó hányadosa,
• A koszinusz függvény (cos) az α szög melletti b befogó és a c átfogó hányadosa,
• A tangens függvény az α szöggel szemben lévő a befogó és a szög melletti bbefogó hányadosa.

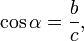
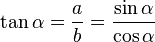
Egy másik módszer a trigonometria megértéséhez az egység sugarú kör ábrája (ábra: Unit Circle). Ebben az esetben polárkoordináta rendszert használunk a korábban használt Descartes-féle helyett. "A polárkoordinátázás a sík egyfajta görbevonalú bekoordinátázása. Koncentrikus körök és sugárirányú egyenesek alkotják a hálózatot". Egy pont helyzetét nem x,y koordináa szerint adjuk meg hanem r és θ adatok alapján, ahol az r a kör sugarát és a θ (théta) a forgás szöge. A szöget jobb középső szélen kezdjük mérni és az óramutató járásával ellentétes irányban mérjük. (Lásd radián ábra). Az egységnyi kör (Unit Circle) diagramban a p pont 45º-nál helyezkedik el ami PI/4 értéknek felel meg radiánban megadva. 180º =  PI . A PI értéke megközelítőleg 3.142.

A polárkoordináta rendszerben tehát nem fokban mérjük a szögeket hanem radiánban. A forgás ívhosszát kiszámíthatjuk  r*θ képlettel, a kör sugarát meg kell szorozni a szögével. De általában ezt a rendszert a pixel koordinátáinak meghatározására szogtuk használni (pl. ha körbe akarunk forgatni egy pontot az origóhoz képest).

"A fenti definíciók (sin, cos, tang egyenletek) csak 0 és 90° között (0 és π/2 radián között) értelmezhetők. Az egységsugarú kört alkalmazva a definíció kiterjeszthető az összes pozitív és negatív argumentumra (l. trigonometrikus függvények). A trigonometrikus függvények periodikus függvények, 180° (π radián) vagy 360° (2π radián) periodicitással. Ez azt jelenti, hogy ismétlődnek a fenti értékekkel." Tehát periodikus hullámként jelenik meg a szinusz és a koszinusz.

A körvonalon fekvő p pont egy háromszögre illyesztehtő, ahol a sugár az átfogó, így alkalmazhatjuk a Pithagorsz tételt. Így tudsz átjárni a két koordináta rendszer között:

  x = cosine(theta) * radius
  y = sine(theta) * radius

Ez a Processingben a következő képpen néz ki:

  float x = cos(radians(angle)) * radius;

   float y = sin(radians(angle)) * radius;

Nefelejtsd el hogy a polárkoordináta rendszerben radiánt használunk még a Descartes-félében fokot! A kettő közötti váltás a következő egyenlettel lehetséges:

  theta = angle*pi/180
  angle = theta*180/pi

De Processingben van egy kényelmesebb megoldás is erre:

  theta = radians(angle)

  angle = degrees(theta)

SZINTAXISOK:

Trigonometry

acos()

asin()

atan()

atan2()

cos()

degrees()

radians()

sin()

tan()

Ahol a szöget PI-ben adjuk meg! A sugarat ki tudjuk számolni a Pitagorasz tétellel:

Radián és fok viszonya:

Szögfüggvények:

Összefüggések: szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg), -ezek a periodikus függvények-  és szekáns (sec), koszekáns (csc):

Trigonometrikus függvények ábrázolása:

http://www.akg.hu/matek/fuggvenyek/sinus.html animáció itt.

PÉLDA

A következő példa azt mutatja be hogyan függössze az egységsugarú kör aszinusz hullámmal:

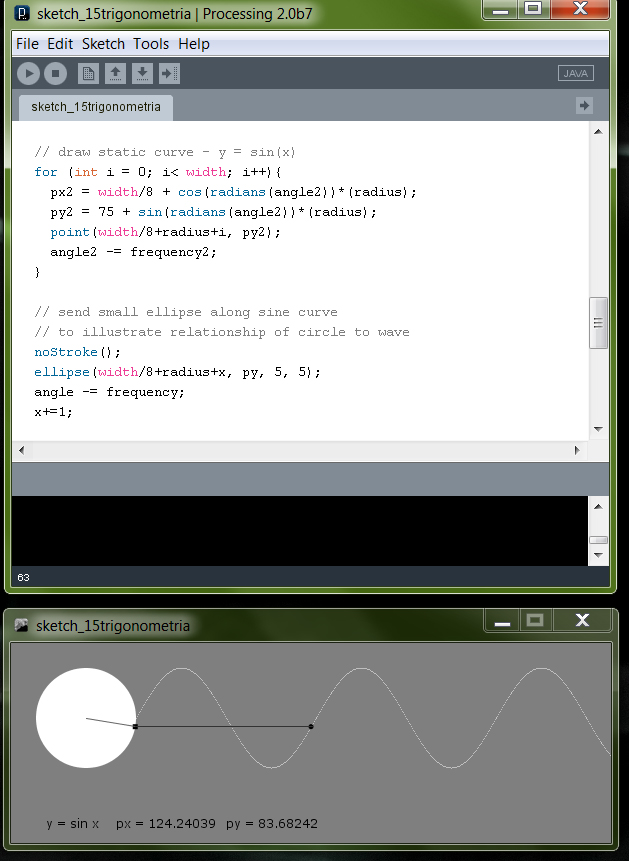
/** Sine Console
* Processing: Creative Coding and
* Computational Art
* By Ira Greenberg */

float px, py, px2, py2;
float angle, angle2;
float radius = 50;
float frequency = 2;
float frequency2 = 2;
float x, x2;

// létrehozunk egy font objektumot
PFont myFont;

void setup(){
  size(600, 200);
  background (127);
  // egy rendszer font-ból generáljuk a betűnket
  myFont = createFont("verdana", 12);
  textFont(myFont);
}

void draw(){
  background (127);
  noStroke();
  fill(255);
  ellipse(width/8, 75, radius*2, radius*2);
  // a kör körül forgatjuk a négyzetet
  px = width/8 + cos(radians(angle))*(radius);
  py = 75 + sin(radians(angle))*(radius);
  rectMode(CENTER);
  fill(0);
  //kirajzoljuk a négyzetet
  rect (px, py, 5, 5);
  stroke(100);
  line(width/8, 75, px, py);
  stroke(200);

  // ismét 0-ra inicializálunk hogy elkerüljük,
  // a villogást az újra rajzolás alatt
  angle2 = 0;

  // kirajzoljuk a statikus görbét - y = sin(x)
  for (int i = 0; i< width; i++){
    px2 = width/8 + cos(radians(angle2))*(radius);
    py2 = 75 + sin(radians(angle2))*(radius);
    point(width/8+radius+i, py2);
    angle2 -= frequency2;
  }

  // a sinus görbe mentén kis ellipszist küldünk
  // hogy illusztráljuk a kapcsolatot a kör és a
  // hullám között:

  noStroke();
  ellipse(width/8+radius+x, py, 5, 5);
  angle -= frequency;
  x+=1;

  // amikor a kis ellipszis az ablakunk végéhez ér
  // újra inicializálunk néhány változót:
  if (x>= width-60) {
    x = 0;
    angle = 0;
  }

  // változó értékű, dinamikus vonallal kirajzoljuk
  // a hullámot:
  stroke(50);
  line(px, py, width/8+radius+x, py);

  // kiküldünk pár számítást az ablakba
  text("y = sin x", 35, 185);
  text("px = " + px, 105, 185);
  text("py = " + py, 215, 185);
}

forrás:

http://hu.wikipedia.org/wiki/Trigonometria

http://processing.org/learning/trig/

http://hu.wikipedia.org/wiki/Trigonometrikus_f%C3%BCggv%C3%A9nyek

http://hu.wikipedia.org/wiki/Trigonometrikus_azonoss%C3%A1gok

http://hu.wikipedia.org/wiki/Pol%C3%A1rkoordin%C3%A1ta-rendszer

http://en.wikipedia.org/wiki/Radian